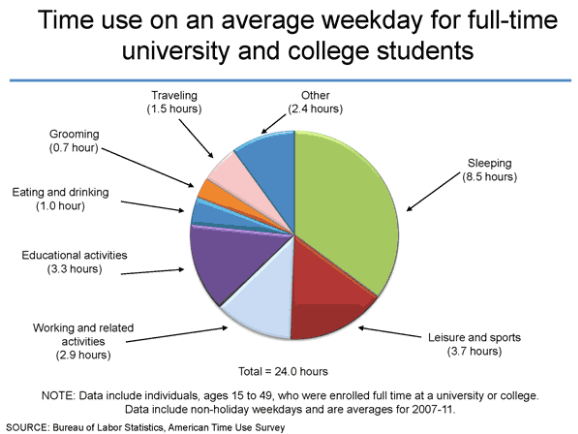
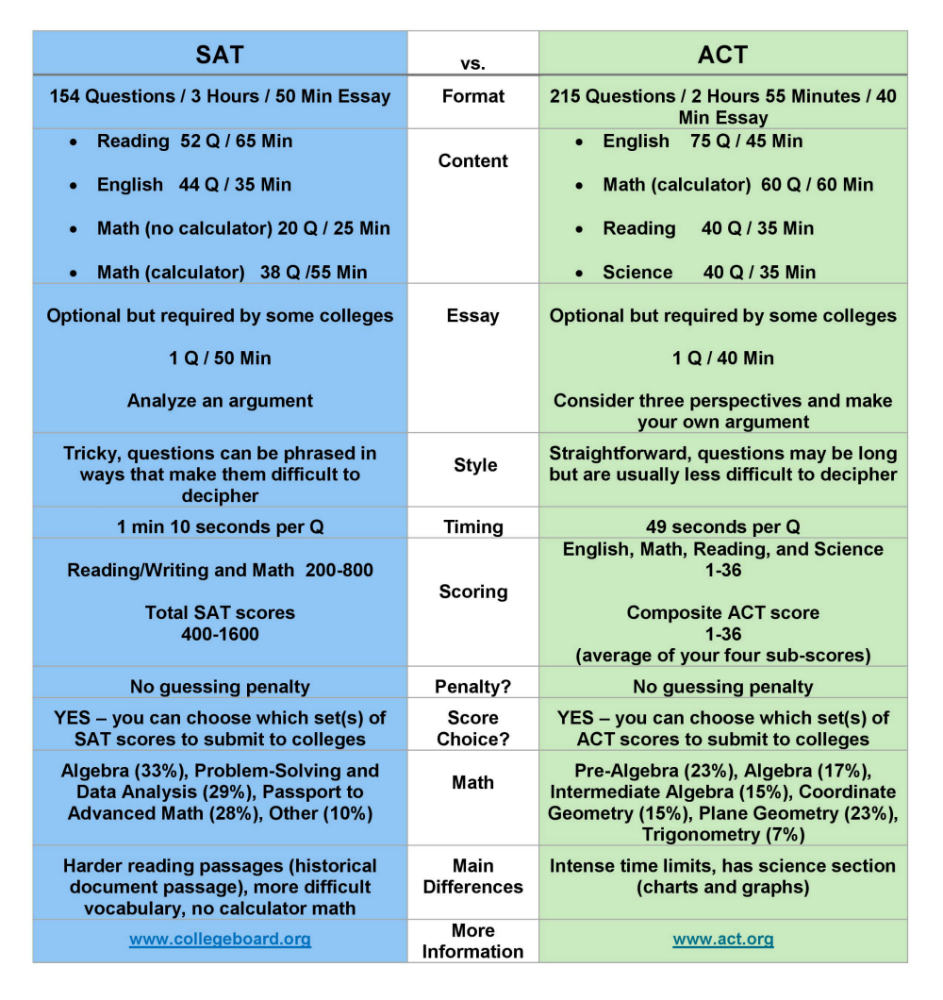
Binary search tree - Programming Homework Helper.
Binary Search Tree is a node-based binary tree data structure which has the following properties: The left subtree of a node contains only nodes with keys lesser than the node’s key. The right subtree of a node contains only nodes with keys greater than the node’s key.
Homework 4: Binary Search Tree You are to code a binary search tree. A binary search tree is a collection of nodes, each having a data item and a reference pointing to the left and right child nodes. The left child node and all of its children are less than the data. The right child node and all of its children are greater than the data.
Homework: Binary Search Trees Name: 1. Use the following binary search tree to answer the questions below. M G D A H K L T R V U W (a) (5 points) What is the pre-order traversal of this tree? (b) (5 points) What is the in-order traversal of this tree? (c) (5 points) What is the post-order traversal of this tree? 2.
Hence the tree after step (e) is a heap and is the desired answer. Textbook 5.32 You must keep track of some data. Your options are: (1) A linked-list maintained in sorted order. (2) A linked-list of unsorted records. (3) A binary search tree. (4) An array-based list maintained in sorted order. (5) An array-based list of unsorted records.
Following there is an example of binary search tree: Advantages of Binary Tree: Searching in Binary tree become faster. Binary tree provides six traversals. Two of six traversals give sorted order of elements. Maximum and minimum elements can be directly picked up. It is used for graph traversal and to convert an expression to postfix and.
Homework 4 - Binary Search Trees Due: Tuesday, September 27 at 5pm Read the expectations on homework. Assignment Goals. To make sure you can write data definitions for binary search trees. To make sure you can write programs over binary search trees. Preliminaries An important variant of the binary tree is the binary search tree. In a binary.
Homework: 1. write out the full set of search trees forthis query to find out what Prolog should produce as solutions for Y. 2. check that Prolog produces the results you thought 3. see if you can following through using trace(k) the steps that Prolog actually went through: are they the same as your proof tree?